編み物は四次元？

佐倉編物研究所の伊藤です。

前回のコラム、思いのほか多くの皆さんに読んでいただけたようで、嬉しい限りです。実は、数学と聞くと拒否反応を示しつつも、怖いもの見たさで気になっている編物愛好家が多いのかもしれませんね。

さて、皆さんは2次元とか3次元という言葉を耳にしたことがあるのではないでしょうか？

2次元とは平面に表現されたもの、3次元は3D（three dimension）とも呼ばれるように、立体的なものを指す、という認識でおおむねよいでしょう（最近は2.5次元というものもあるようですが）。

次元というものを感覚的に理解できる人も多いかと思いますが、数学的に大雑把に言うと、ある状態を表すために必要な変数の数を次元と呼んでいます。

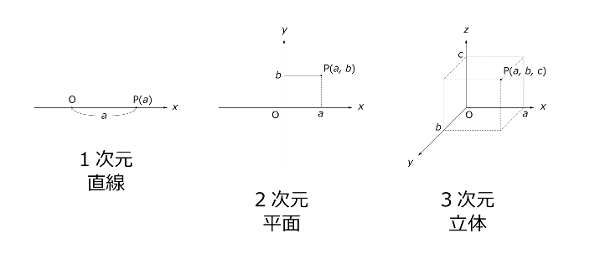
中高の数学をちょっと思い出していただくと、1次元とは、1つの数で表される状態のことで、身近な例で言えば数直線、つまり線を表します。数直線上の1点を指定するには、その目盛りを読めばよいので、1つの数（変数）で表すことができます。

つまり1次元。

2次元とは、たとえばx軸とy軸で表される平面を表します。この座標平面上の点を指定するには、（x, y）の2つの変数が必要ということで、2次元と言います。

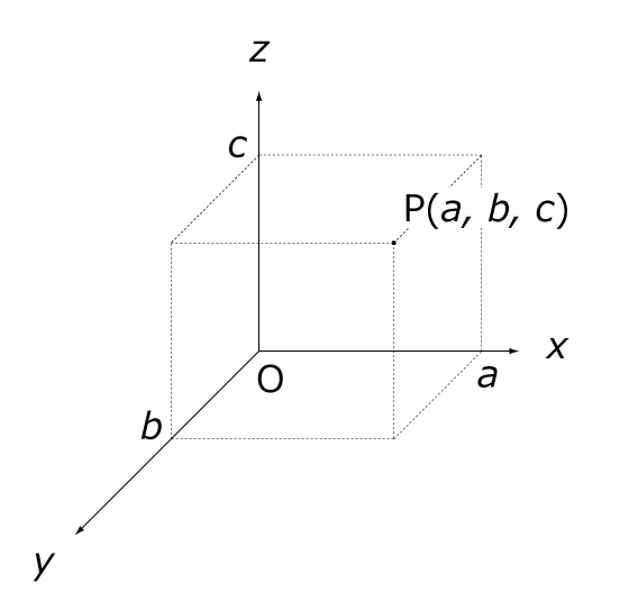
3次元とは、x軸とy軸に加えて、z軸で表される空間に広がり、立体を表すことができます。空間上の1点を指定するには、（x, y, z）の3つの変数が必要ということで、3次元なのです。

これを踏まえて、編み物のことに思いを馳せてみましょう。

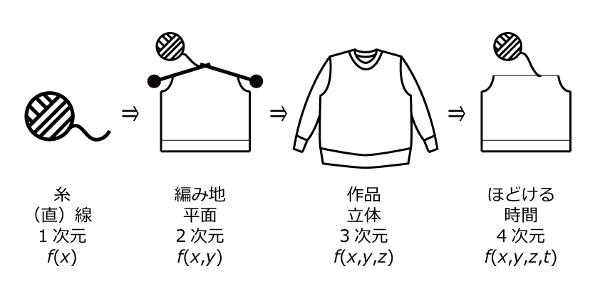
毛糸。かなり乱暴ですが、ひとつの線と考えることができます。つまり、毛糸そのものは1次元的です。編み物は、編み針を用いて毛糸を編んでいくわけですが、その多くの場合、編み地という平面ができあがります。つまり、毛糸を編むと2次元的になります。

その編み地をとじ・はぎなどを駆使すると、セーターなどの立体作品になります。つまり、そういった作品は3次元的なものなのです。そしてここからが肝心です。

編み物は糸を引くと、するするとほどける、つまり前の状態に戻すことができますよね？

これ、数学的というか物理学的な観点から見ると、時間(t, time)が戻ると解釈することができます。この時間tという変数が、3次元のx, y, zの3変数にさらに加わる4つ目の変数ということで、4次元的と言うことができます。

よって、編み物は4次元の手仕事と表現できるのではないでしょうか。

4次元の手仕事、なんだか響きが理系チックで格好良くないですか？

編み物のことを語るときに、枕としてよくこの話をしています。

 ほどけば元に戻せる（時間を戻せる）というのは編み物の大きな特徴と言えます。もちろん他の手仕事にも元に戻せるものはありますが、編み物がとりわけ特徴的なのは、糸を引けばするすると簡単に戻すことができるということです。

ほどいて元の糸に戻るという性質を利用して、大人用のセーターを子ども用に編み直したことがある人もいるのではないでしょうか。かつては、毛糸がとても貴重だったので、一度編んだ作品をほどいて糸に戻し、別のものに編み直すということが当たり前にされていたようです。

今は毛糸があふれるほど供給されているので、このようなことはほとんどされていないかもしれませんが、この4次元の性質というのは、資源・素材の再生利用という持続可能性の話につながっていく訳です。

編み物の4次元的性質が、数学的な話から社会的な話に広がっていきましたね。

 なお、数年前から、SNSでは、編んだものをほどくことを「製麺する」と言うスラングが流行っているようです。なんでも、ほどいた直後のくしゃくしゃになった毛糸が、まるでちぢれ麺のように見えるからなんだとか！