
目次
1. 長編みで円盤を編む
2.フリルを幾何学的に見る
3.アメリカの数学者がかぎ針編みで双曲面を表現
4. 実際に双曲面を編んでみた
5. おわりに
佐倉編物研究所の伊藤です。
突然ですが、夏素材などで底面が円盤型のバッグをオール長編みで編むことを考えてみてください。
1. 長編みで円盤を編む
「わ」の作り目で始め、立ち上がりの鎖3目を編み(これは長編み1目分になる)、1段めに長編みを何目か編んで1周するのですが、さて、何目編みますか?
デザインによっていろいろあるのですが、16目? 15目? それとも17目?
2段めは、1段めのそれぞれの編み目に長編みを2目編み入れて1周します。すると、編み目の数が1段めの2倍になります。
3段めは「長編み1目単独、長編み2目編み入れる」を繰り返して1周。つまり、編み目の数が1段めの3倍になります。
4段めは「長編み1目単独、長編み2目編み入れる、長編み1目単独」を繰り返して1周。
その結果、編み目の数が1段めの4倍になります。
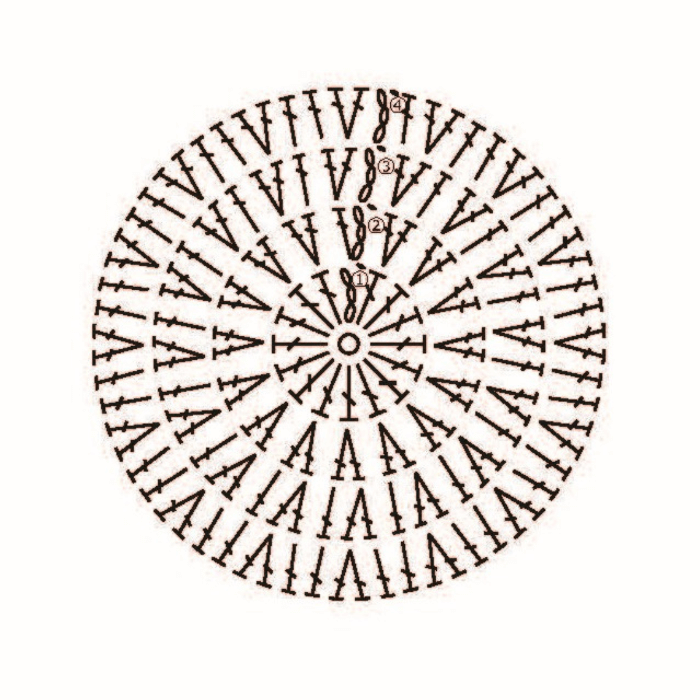 1段めが16目のときの記号図
1段めが16目のときの記号図
さて、1段めに編み入れる長編みの目数(立ち上がりの鎖3目も長編み1目分としてカウントする)を何目にするかによって、編み上がる形に少し変化が現れます。
私のこのとき1段めの長編みの目数は下の画像の左(茶色)が15目、中央(白)が16目、右(グレー)が17目で編み始めています(リッチモア パーセント、かぎ針6/0号使用)。

16目で始めた白は、ほぼ平らな円盤状に編み上がっています。一方で、1目少なくした茶色は縁が少しせり上がっていて、お椀状になっています。このまま編んでいくとお猪口のようになるでしょう。
1目多くしたグレーは、縁が波打っていて、このまま編んでいくとまるでフリルのような状態になるでしょう。もちろんこれは、長編みの編み目の高さと幅のバランスによって、円盤になるのが何目なのかが変わってきます。
また、1段めの目数をもっと減らすとさらに早くお猪口型になり、もっと増やすとさらに激しくフリルが現れることになるでしょう。平らな円盤を編みたいのに、見極めを誤ると上の茶色やグレーのようになって「あ、おちょこんなっちゃった」「あ、フリルんなっちゃった」と嘆いて最初からやり直すことになります。
2.フリルを幾何学的に見る
目数を多くすることで現れたフリルに着目してみます。
編み物でフリルを表現するには、今見てきたように、平たく編み上がる場合よりもたくさんの増し目を途中で行います(分散増し目)。こうすることで、面が波打ってフリルの形が現れてきます。
このフリルの面の形、幾何学的な用語で言うと「双曲面」というものになっています。
ちょっと難しい話になるので詳しいことは専門書に譲りますが、平面の曲がり具合を曲率といい、それが正(プラス)である面を曲面、ゼロである面を平面、負(マイナス)である面を双曲面と呼びます。
イメージとしては、以下のような感じです。
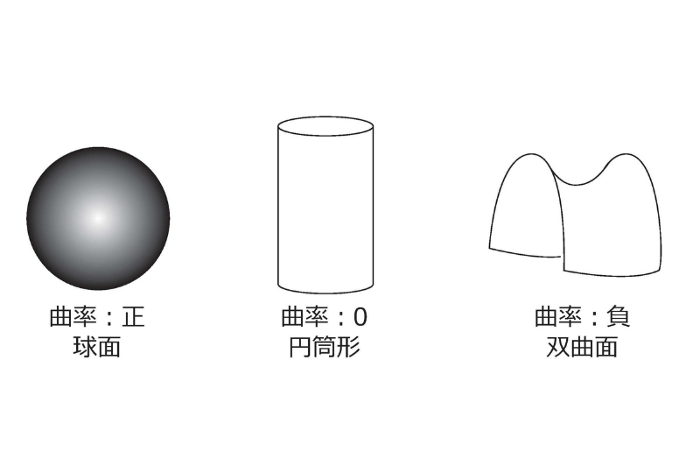
球とかレンズなどの表面が曲率プラス(正)の球面、まっ平らな面や円筒形の表面が曲率ゼロの平面、乗馬の鞍やズボンの股ぐりなどの形が曲率マイナス(負)の双曲面、というイメージです。ここで、先の方法つまり分散増し目で作られたフリルは、双曲面の形をしているのだそうです(詳しくは後述)。
では双曲面とはいったい何でしょう?
小中学校の算数・数学の授業で、みなさんは次のようなことを学んだかと思います。
a-1)三角形の内角の和は180°である
a-2)ある直線ℓに対し、ℓ上にない点を通りℓに平行な直線は1本だけ引くことができる
これは曲率ゼロの平面上では成り立つが、双曲面上では成り立たず、代わりに以下のことが成り立ちます。
b-1)三角形の内角の和は180°よりも小さい
b-2)ある直線ℓに対し、ℓ上にない点を通りℓに平行な直線は何本も引ける
このように、みなさんにはなじみのあるa-1), a-2)が成り立たないようなヘンテコな世界が、フリルの上では繰り広げられているのです。
ちなみに、曲率プラスの曲面では、以下のことが成り立ちます。
c-1)三角形の内角の和は180°よりも大きい
c-2)ある直線ℓに対し、ℓ上にない点を通りℓに平行な直線は引くことができない
そして曲率ゼロの平面上で展開される幾何学を「ユークリッド幾何学」、双曲面(曲率マイナス)、曲面(曲率プラス)上で展開される幾何学を「非ユークリッド幾何学」と呼んでわけています。
3.アメリカの数学者がかぎ針編みで双曲面を表現
ではフリルが双曲面を形成するというのはどのようにして示されたのでしょう?
ラトビアの女性数学者Daina Taiminaがコーネル大学で教鞭を取っていた1990年代末、かぎ針編みの造形が双曲幾何学のモデルを説明するのに適していると発見したのが始まりでした。
彼女は、たとえば細編みを4目編んで次の目で2目編み入れて増し目をするというセットをどんどん繰り返すことにより、双曲面の造形が現れるということを説明しました。それが双曲面であることを平行線の公理(先のb-2)の性質)を実際に編み地の上で毛糸を用いて線を引くことにより示しました。
さらに、オーストラリア生まれのサイエンスライターMargaret Wertheimは、2005年から始まった珊瑚を生み出すプロジェクトの中で、世界中のクロシェターが編んだかぎ針編みの双曲幾何学珊瑚で空間を埋め尽くす活動をしてきました。
それに付随する講演の中で、MargaretはDainaのかぎ針編みと双曲幾何学の研究に触れ、かぎ針編みという手仕事が、数百年も数学者を悩ませてきた抽象的な概念にはっきりと形を与えたということを述べています。以下に、それについて語られた動画があります。
https://www.ted.com/talks/margaret_wertheim_the_beautiful_math_of_coral?language=ja&subtitle=ja
(字幕を日本語に設定できます)
なんと、かぎ針編みが数学の研究の大発見の助けになったというのです。
フリルのような双曲面は珊瑚だけでなくある種のレタスの葉の縁や、きくらげ、ウミウシ、ケイトウの花など自然界に元から存在しているということを、改めて気づかせたわけです。
4. 実際に双曲面を編んでみた
Dainaによると、「ある一定の割合で増し目をし続けていけば、その編まれたものを全体としてみると双曲面になっている」ということです。これは冒頭に円盤のモデルを考えたときに、すでに出てきていました。
では改めてちょっと極端な条件で実際に双曲面を編んでみましょう。もういっそのこと増し目をしまくって、どんな形になるのかを見ていきます。
今回はカラフルなこんな糸を使いました(Opal Holidays、かぎ針6/0号使用)。

まずは1段め。わの作り目をして、長編みを3目編み入れます(最初の1目は立ち上がりの鎖3目)。

2段め。1段目の編み目それぞれに、長編みを3目編み入れます。2段めの目数は3×3=9目。

3段め。同様に、前段の編み目一つ一つに長編みを3目ずつ編み入れます。目数は3×3×3=27目。

4段め。同様にして、目数は3×3×3×3=81目。フリルっぽさが出てきました。

5段め。目数は3×3×3×3×3=243目。さらに激しくフリフリになってきました。

6段め。目数は3×3×3×3×3×3=729目。なんだかもうフリルというより…脳みそ?

7段めになると、目数は3×3×3×3×3×3×3=2187目にもなります。
私はもう疲れてしまったし、きっと脳みそっぽさはもう変わらないでしょうから、このくらいでやめておきます。
今回は長編みで、すべての目に3目編み入れるタイミングで編んでいきましたが、細編みなどにしたり(Dainaさんはもともと細編みで編んでいた)、増し目のタイミングを変えたりすると、でき上がりはいろいろ変わっていくようです。いずれにしても、Dainaさんが示したように編み地の表面は双曲面を成しています。
5. おわりに
かぎ針編みの増し目でできるフリルの先には、アカデミックな世界とのつながりがあったり、自然界の造形があったり、普段ただ編み物を楽しむだけでは想像もしなかった世界が広がっています。
なお、この双曲面の造形は、布や紙などでは実現困難で、編み物ならではのことだということです。
やっぱり編み物すごい!
参考文献:
“Crocheting Adventures with Hyperbolic Planes: Tactile Mathematics, Art and Craft for all to Explore, Second Edition (AK Peters/CRC Recreational Mathematical Series)” Daina Taimina, CRC Press(2018).
https://www.amazon.co.jp/Crocheting-Adventures-Hyperbolic-Planes-Mathematics/dp/0367375079
千葉県生まれ。 東京大学理学部卒業・同大学院修士課程修了(理学修士)。佐倉編物研究所所長。化学メーカー、理工学専門書出版社などの職を経て、2010年よりヴォーグ学園東京校で本格的に編み物を学ぶ。手あみ師範の資格を取得後、毛糸メーカーに就職し、企画・デザイン、講師、バイヤー、営業などの業務に携わる。独立後、地元で佐倉編物研究所を開所。各所で編み物講習を開くほか、書籍・雑誌に作品・デザインを発表するなど、活動の幅を広げている。2020年1月トークショー「あみもの夜話第4話『編み物と数学』」ゲスト出演(MC:横山起也氏、浅草橋Keitoにて)。2022年2月NHKすてきにハンドメイドに「ぷっくりハートモチーフ」の講師として出演。
https://ameblo.jp/sakuraknittinglab/


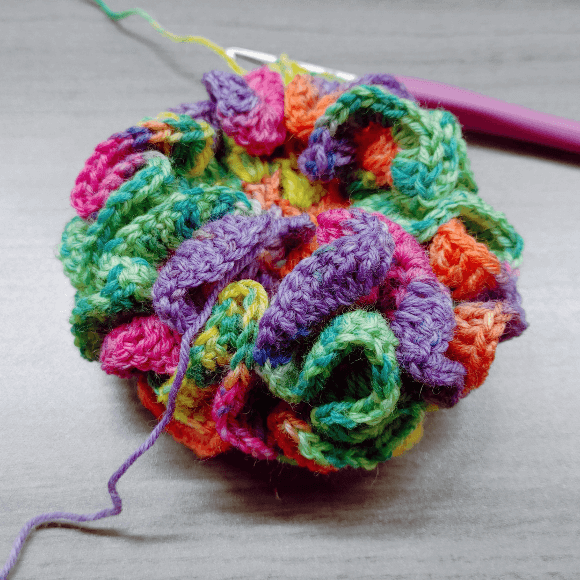

 ポスト
ポスト