編み物と数学

佐倉編物研究所の伊藤です。

どういうわけか化学の研究の世界から編み物の世界に飛び込んできた、異色の存在と言われています。

「なぜ編み物をしているんですか？」

「どうしてそんなに編み物に熱中しているんですか？」

よく聞かれます。編み物をする男性はまだまだ少数派、みなさん興味があるのでしょう。こう答えます。

「編み物の数学っぽいところに惹かれたんです」

すると、多くの人はこう反応します。

「えっ、数学？　はぁ、そうですか…（なに言ってんの、このひと）」

おそらく多くの編み物愛好家は、ファッションだったり、編んで作る小物や雑貨が可愛いからということで、編み物の世界に入ったのではないでしょうか。そういう人からすると、「え？　数学？　…なんで？」と思うのも当然でしょう。あるいは、編み物に何となく算数とか数学の影がちらついているとうすうす気づいている人もいると思いますが、それでもやっぱり何となく数学というものに拒否反応が出て、なるべく関わりたくないと思ってしまうようです。

それでも、編み物に深く携われば携わるほど、数学と編み物には強い関わりがあるということに気づかされていきます。では、具体的に編み物にはどういう数学が関わっているのでしょうか？

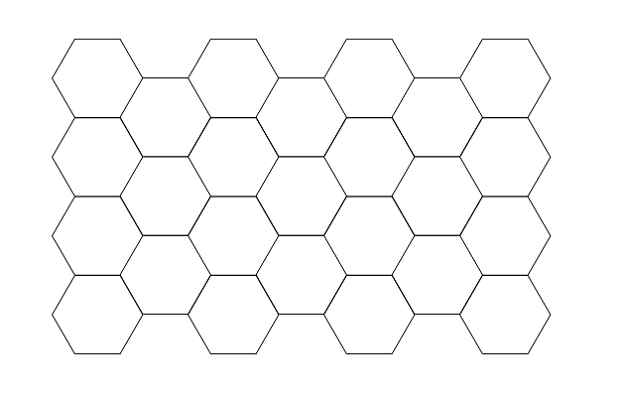
たとえば、モチーフつなぎ。もし1種類の正多角形のモチーフを使って平面のモチーフつなぎの編み地を作ろうと思ったら、以下のように正三角形、正方形（正四角形）、正六角形の3パターンに限られます。

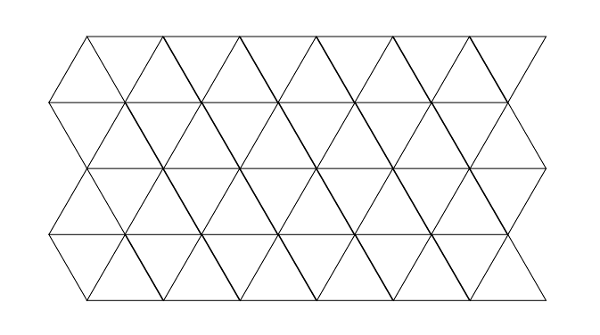
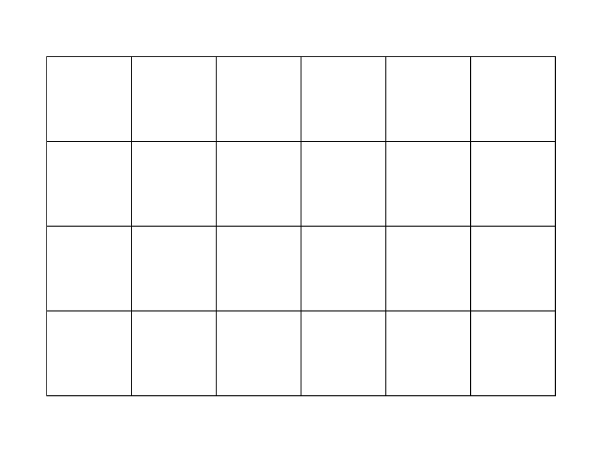
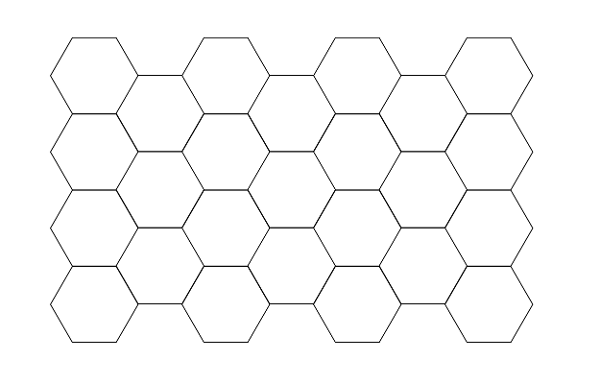
複数種類の正多角形を用いてもよい場合は、たとえば以下の正八角形と正方形の組み合わせなど、全部で8パターンあります。

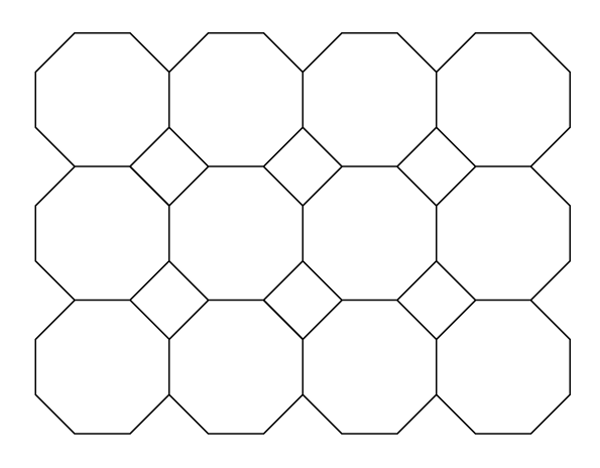
こういったことは、数学のうちの「幾何学」（図形をおもに扱う数学）という分野の、さらに「平面充填」とか「テセレーション（tessellation）」という領域の知識や感覚が関わってきます。幾何学という数学が関わっているということを強く意識すると、モチーフをつなぐときに腕がいくつないといけないとか、どことどういうつなぎ方をしなければならないとか、正確にモチーフつなぎをする一助になるだけでなく、自分でモチーフつなぎの作品をデザインするときの役にも立つことになります。

もうひとつ、たとえば、以下のようなかぎ針編みの模様編みを考えます。

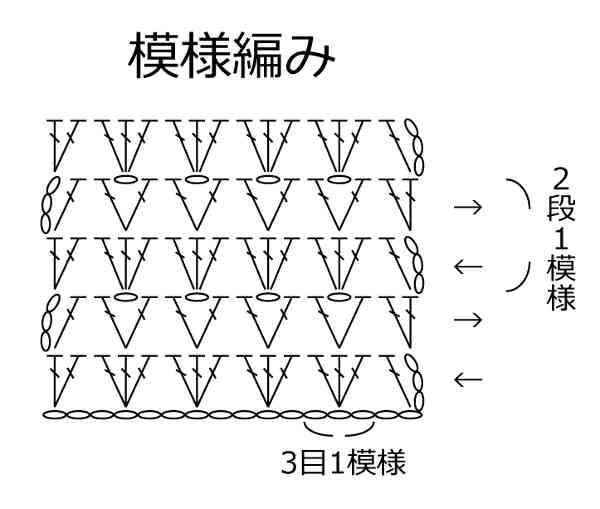
この模様編みは、3目1模様の構造をしていて、3目の繰り返し（リピート）によって模様が広がっていきます。この「繰り返し」というのが、数学ではよく出てくる要素です（周期関数、数列などなど）。そして、この模様を用いて平編みで編み地を作るとき、作り目は「3の倍数＋1」目と表現されます。このプラス何目というのは、模様によって変わってくるのですが、いずれにしても「対称性」という数学の要素を考慮に入れて出てくる結果です。

さらに言うと、編むときはよほどイレギュラーな状況でない限り、必ず「数えて」いますよね？数えるということは、数学（算数）の最も基本的な動作のひとつです。ほら、編むということは、ほぼ同時に数学もやっているようなものなのです。

編み物がよくできる方々と編み物の話をしているときに数学のことを持ち出すと、「あたし数学苦手だから…」と悲しい顔をしてしまう方がいらっしゃいますが、私はそうは思いません。それだけいろいろなものを編めるのであれば、数学が苦手なのではなくて、実は知らないうちに数学のセンスが身についていると言えます。あるいは、編み物をしながら数学的な訓練も同時にしていると考えることができるのではないでしょうか。

ですから、ちょっと視点や考え方を変えて編み物をしていただけたら、また別の楽しみ方や別の広がり方があるのではないかと思います。今後、このコラムでそういったことに気づくことができる話をいろいろできたらと思います。

そういえば、長年編み物ばかりやっていたため、すっかり身体がなまってしまいました。いまは典型的なオッサン体型です。そこで、無謀ではありますが、最近なわとびトレーニングを始めました。全身の筋肉が鍛えられるということですが、持ち手を持ってなわを回し続けるので手首回りの強化にもつながるそうです。編む操作の安定性にもつながるかも…？　人体実験です。

1.「大人になってから再学習　平面充填　－　はてなブログ」

https://zellij.hatenablog.com/entry/20130202/p1

2.「かぎ針あみ 割り出し法①基本の編み目と使いやすい模様編」日本ヴォーグ社より